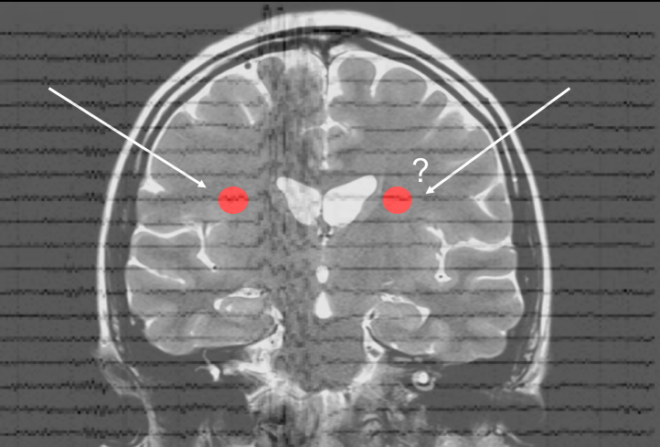
LCMV Beamformers are a type of beamformer algorithm used source estimation from EEG data.
In the previous blog post we saw how beamformers can be used for source estimation from EEG data. To recap, the beamformer method is a spatial filtering technique where the idea is to choose weights in such a manner that only the signal from a desired location is enhanced. In a particular class of beamformers, known as LCMV beamformer, which is widely used in EEG source estimation, the aim is to choose the weights such that the output variance of the beamformer is minimized, under the constraint that only the neural signal from the desired location is passed. A volumetric image of source power can be created by sequentially applying beamformer to a number of pre-specified locations or every location on the source space (i.e. the brain). The regions with high variance in source power can be interpreted as contributing to most of the EEG/MEG measurements, while regions with small variance can be considered inactive.
Assumptions and their implications
The LCMV beamformer makes two main assumptions (note that both assumptions come with caveats and their relevance can be debated, but for the purpose of illustrating this algorithm, let’s assume they hold true)
- Neural sources can be sufficiently modelled as dipoles.
- The time-courses of the neural sources to be estimated are uncorrelated
Assumption 1) restricts the estimation of neural sources that have considerable spatial extent (i.e. a larger area of the cortex is active). In practice, this suppresses the output of the beamformer, as the spatial extent of the active cortex increases. In a study by Vrba [1], using simulations (spherical head model), it was shown how the spatial extent of the sources can affect the beamformer output. Spatially extended sources (length = 1 cm) were modelled using 50 equally spaced dipoles, with correlated activity. As seen in the below figure, for small source strengths (< 50 nano Ampere-meters), we can see that the normalized beamformer output (Z), where the normalization is done using the noise power, for both point-like source and spatially extended source (spatial extent of 1 cm), is indistinguishable, as signal is mainly dominated by noise (this is akin to low SNR condition). As the source strength increases, the output of the beamformer increases linearly for point-like sources, whereas for extended sources, it starts to decrease.
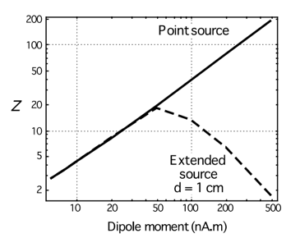 Figure 1: Sensitivity of extended and point sources of variance beamformer [1]
Figure 1: Sensitivity of extended and point sources of variance beamformer [1]
The implication of the second assumption (2) is that the output power of the beamformer is attenuated if two highly correlated sources are present and in this scenario little or none of the original source power is recovered. As seen from a simulation study in the figure below from [2], where the Y-axis represents the diagonal elements of the normalized source covariance matrix, which can be interpreted as the source power given as beamformer output, when the correlation between the sources increase, the source covariance goes to zero, implying the sources are not detected by the beamformer. For the perfectly uncorrelated sources (0% correlation), the source covariance is maximum. It is also seen that when the sources are partially correlated (shown in green), the beamformer output is reduced due to signal cancellation, but the sources may still be detected depending on how strong the cancellation is. Effect of correlated sources on the performance of beamformers have been demonstrated for example in bilateral activation of the temporal lobes during steady-state auditory stimulation [3,4,5].
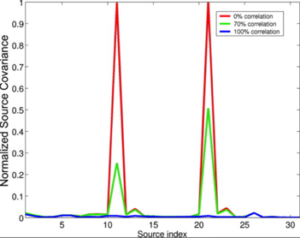
Figure 2: Dependance of normalized source covariance on source correlation [2].
Other formulations of beamformer
To overcome the limitation of the minimum variance beamformers, several variations have been proposed [6], all of which cannot be discussed here. Brookes and colleagues proposed a dual-beamformer approach [3], which is a simple extension of the original LCMV beamformer, which aims to find weights for one location at a time. Instead, in the dual beamformer, the weights are sought for linear combination of two source lead fields and thus beamformer minimizes power originating from locations other than the two locations defined. It is in principle possible to apply this method to a large number of sources, but this can lead to very high computational cost due to search over all possible source combinations. Moreover, the recovered source time course is a linear combination of the time courses of all the sources involved and finding individual time courses involves estimating weighting parameter through optimization techniques to find the relative weighting of the individual signals. This can be particularly problematic as the number of sources increase. One way to mitigate this problem could be to have some a priori knowledge about the possible source locations [3] rather than to do an exhaustive search, but such information is seldom available or is dependent on other modalities such as fMRI.
The figure below from [3] shows the localization of correlated sources from MEG data pertaining to simple auditory stimulation, in the left and right auditory cortex, where the dual source approach (shown in right) outperforms the traditional single-source LCMV beamformer (shown in left).
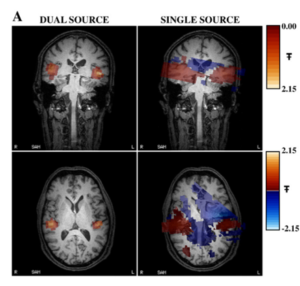
Figure 3: An example comparison of localization results using dual source and traditional LCMV beamformer.
Instead of using the linear combination of lead fields pertaining to two sources, several researchers have proposed to use the lead field solution of two (or more) sources together in order to find the optimal weights and these approaches come under the class of multiple constraint minimum variance (MCMV) beamformers [6]. One such approach is the dual-core beamformer proposed by Diwakar and colleagues [7], which uses a lead field matrix of two sources simultaneously. Again, when there is no a priori information about the source locations, an exhaustive search over all possible dipole combinations must be performed (for n dipoles this amounts to n(n-1)/2 combinations). The advantage of this approach over the approach proposed by Brookes and colleagues is that the optimization of the source orientation and their relative weighting (for linear combination) need not be performed, as the lead field of both the sources are combined. Moiseev and colleagues proposed MCMV based iterative source localizers that can recover multiple correlated sources (< 10) with reasonable computational effort [7].
In summary, although beamformers are advantageous in terms of their localization accuracy and spatial resolution combined with moderate computational cost (which increases with the number of sources), it is important to be aware of the assumptions that they make, which include point-like sources and uncorrelated sources. Although approaches have been proposed to deal with correlated sources, such approaches can recover only a small number of sources (< 10). However, beamformers are a useful approach when there is a strong reason to believe that sources are mostly uncorrelated or correlated only for a short time and the MEG/EEG data is generated by reasonably few sources.
References
[1] Vrba, J. “Magnetoencephalography: the art of finding a needle in a haystack.” Physica C: Superconductivity 368.1-4 (2002): 1-9.
[2] Hillebrand, Arjan, et al. “A new approach to neuroimaging with magnetoencephalography.” Human brain mapping 25.2 (2005): 199-211.
[3] Brookes, Matthew J., et al. “Beamformer reconstruction of correlated sources using a modified source model.” Neuroimage 34.4 (2007): 1454-1465.
[4] Popescu, Mihai, et al. “Spatio–Temporal Reconstruction of Bilateral Auditory Steady-State Responses Using MEG Beamformers.” IEEE Transactions on biomedical engineering 55.3 (2008): 1092-1102.
[5] Herdman, Anthony T., et al. “Determination of activation areas in the human auditory cortex by means of synthetic aperture magnetometry.” Neuroimage 20.2 (2003): 995-1005.
[6] Moiseev, Alexander, et al. “Application of multi-source minimum variance beamformers for reconstruction of correlated neural activity.” NeuroImage 58.2 (2011): 481-496.
[7] Diwakar, Mithun, et al. “Dual-core beamformer for obtaining highly correlated neuronal networks in MEG.” NeuroImage 54.1 (2011): 253-263.