The theory of evolution and the Hodgkin-Huxley model of the action potential are two successful theories in biology that are relevant to the brain. Why have they been successful?
In my preceding posts, I discussed the lack of a successful theory about the brain-mind relationship, the challenges of post-hoc explanations provided by connectionist models, and a broad framework for constructing a successful theory. However, this does not mean that there are no successful theories out there about other big and small aspects relating to the brain that have managed to push empirical research forward. This post begins to inspect these successful theories.
Out of the proven successful theoretical achievements I have already mentioned the feature binding theory by Anne Treisman, when discussing the problems of perception. Hence, I will not discuss this one here. Also, I will not discuss the classical textbook cases of successful theories in physics, as this entire discipline is fairly distant from the biological world—and thus, there is only so much that we can learn from them.
Theory of evolution
The first one that I want to inspect is Darwin’s theory of evolution. This theory applies to biology in general and the brain and behaviour are only a small subsection of its domain of influence. But the theory of evolution has been one of the most successful and useful theories in brain science and psychology. It has guided neuroscience in numerous ways, including understanding the phylogenetic drivers of the developing brain and mind, and enabling cross-species comparisons. In the behavioural sciences, there is an entire field of research driven by the theory, called evolutionary psychology.
So, what are the properties of the theory of evolution that has made it so successful? First, it has created an explanatory domino effect, which is a highly desirable feature; starting with only a small number of assumptions: inheritance, mutation and survival of the fittest, a huge set of data could be explained in respect to both the variety within the animal and plant kingdoms and the similarities between them. Importantly, there was no need to engineer new conflicting assumptions when exploring answers to new questions. For example, whatever it took to explain the evolution of fins in fish did not conflict with an explanation of why flowers were colourful, or how the human brain evolved. And of course, the theory had a spectacularly strong prediction, which was testable and could have either falsified the theory or advanced the science of biology big time; this prediction was about the existence of genes which turned out to be correct and ended with the discovery of DNA.
Since its inception by Darwin in 1859, the theory of evolution has improved and broadened, and a few things are under discussion and consideration to be adjusted. The theory is thus a great example of a productive theoretical construct.
Generation of action potentials
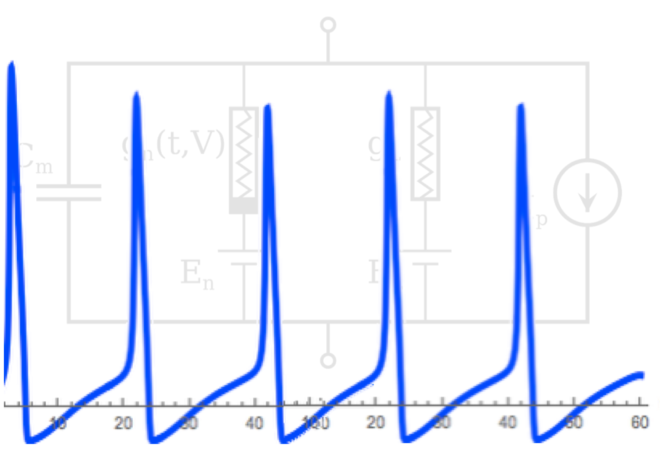
The next theory that I would like to mention is the Hodgkin-Huxley (1952) model of how the action potential is generated across a neuronal membrane. This is a computational theory i.e., it uses equations to describe a fundamental measurable behaviour of neurons. In fact, it uses 14 or so differential equations. So, it is not particularly simple and easy to understand. And yet it is successful. For example, it was instrumental in the discoveries of ion channels and ion pumps—again, based on predictions of the theory that could either make it or break it. Today, any study of nerve cell electrophysiology is impossible without considering the vast knowledge of membrane physiology that has been accumulated and stands on the shoulders of Hodgkin and Huxley’s Nobel prize winning work (the domino effect!).
So, what is it that makes the theory so successful? What makes this computational theory better than connectionist models, which are also computational theories? What did Hodgkin and Huxley do particularly well?
 Figure: Basic components of the Hodgkin-Huxley model
Figure: Basic components of the Hodgkin-Huxley model
I think that the answer lies in how successful vs. unsuccessful theories treat assumptions. To explain new data, every theory must assume some new descriptive parameters or state of affairs. It can be simply a number or something more elaborate such as an equation or a whole matrix of numbers. For example, connectionist models usually need a novel pattern of connections to endow the network with a novel form of behaviour. These can be expressed as numbers in the form of connectivity matrices. The Hodgkin-Huxley model requires new parameters too. So, where is the difference then? The difference is that the equations of the Hodgkin-Huxley model are fixed, while the parameters are changeable. The Hodgkin-Huxley model then treats those changing parameters as strong predictions and stands behind the numbers as if they describe something real. Thus the parameter values allow the model to be applied to different problems. But as soon as a well-fitting value of a parameter is found, the parameter value is used as a prediction. For example, if a new parameter value is needed for membrane permeability for a certain type of ion—then this predicts that a new type of channel must exist on that particular membrane. This is something that can be empirically tested. And has been tested. And discoveries have been made. This is how a successful theory works.
In contrast, connectionist models do not call for tests of their newly assumed connectivity matrices. Moreover, it is often already known upfront that the simulated connections do not correspond to anything that we can find in anatomical atlases. There is already a discrepancy at the very beginning. Consequently, there is no attempt to resolve it afterwards. Connectionist models accept those discrepancies. The Hodgkin-Huxley model does not. Rather, the Hodgkin-Huxley model treats any discrepancies as testable predictions. This approach of the Hodgkin-Huxley model is a much better recipe for a creating a successful theory.
Reference:
Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of physiology, 117(4), 500-544.
To see the entire blog series by Danko Nikolić click here.