Solving the inverse problem in EEG to identify the source of a signal requires a number of assumptions to constrain the solution space. These assumptions have pitfalls that can significantly impact the results.
The Inverse Problem
In many fields such as engineering, physics or applied mathematics, modeling involves predicting the effects or results for a set of known parameters. This is known as forward modeling or forward problem. When solving an inverse problem, we typically start with the results or measured data and then go on to infer what parameters ‘caused’ those measurements. Unlike in a forward problem, the inverse problem has no unique solution i.e., multiple (in theory infinite) set of parameters might explain the same measurement data.
 Image taken from [1]
Image taken from [1]
How does this apply to EEG?
One aim of an EEG inverse problem is to find the location of the signal that is responsible for the measured EEG data. Such solutions are can be extremely useful and important both in clinical neuroscience, for example to aid in the localization an epileptogenic foci and basic neuroscience to enhance our understanding about regions responsible for various cognitive tasks. This requires constructing a ‘source model’ applied to a model of the head.
See related post What does the EEG Signal Measure?
Assumption about the EEG
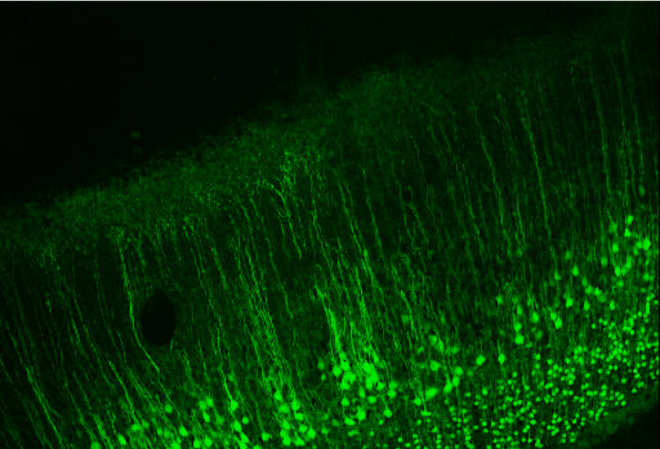
Given that the solution to an inverse problem is not unique, to solve an inverse problem with many unknowns one must first begin with a set of assumptions about how the signal is generated that are at least reasonable. These assumptions essentially impose ‘constraints’ on the problem that reduce the solution search-space. The first assumption is that much of the EEG signal that is measured on the scalp is generated by the pyramidal neurons that are all oriented perpendicular to the cortical surface (see below and main image on top).

Image taken from [2]
Since the apical dendrites of these pyramidal neurons are all parallel to each other in sheets, the excitatory postsynaptic potential (EPSP) in these dendrites should in theory nicely sum across space and time and can be approximated as a current dipole as positive ions (like Na+ or Ca2+) entering the dendrite makes that part of the dendrite positive (creating an extracellular sink) and consequently the other end of the dendrite is negative (creating an extracellular source). Models therefore assume a dipole approximation (blue arrow). Further since currents in a conductor typically form a closed loop, it is assumed that there are also return currents (red arrow), that close the loop.
This return current is assumed to arise because the cerebrospinal fluid and the tissues covering the brain such as the dura, skull and scalp all conduct electric currents. The conductance by these tissues and fluids outside the cells, known as volume conduction, also has to be estimated.
These assumptions that the neural sources or dipoles exist only on the cortical surface and are perpendicular to it then impose a constraint on the EEG inverse problem, reducing the solution search-space only to the cortical surface. These constraints are then translated into a source model that can take several approaches.
Assumption Pitfalls
Even as these proposed models are best approximations it is important to be aware that they are based on assumptions that may be incomplete. First, in reality the flow of current in dendrites is not unidirectional as there are backpropagating action potentials. Further glial cells are excluded from these models even though they significantly outnumber the neurons and have shown to modulate neural activity and actively buffer extracellular potassium concentration [3]. Recent studies (in mouse) have shown that alterations in EEG signals in gamma frequency can be caused by selective expression of neurotoxins in astrocytes [4]. Both these phenomena can substantially alter the source properties of the signal and are yet not fully understood.
See related post Einstein, Astrocytes and the EEG
Further, conductivity values have been shown to have significant impact on the solution to EEG inverse problem and it is extremely difficult to determine conductivity values of tissue like the skull which varies both inter and intra-individually. The conductivity of tissue between the brain and scalp surface is not known as it has thus far not been measured in living tissue. Some studies have measured skull conductivity in vitro using a fresh sample of skull in saline water. However such an approach cannot be used routinely. Further it measures conductivity only on a part of the skull, which brings us to the next issue of inhomogeneity. Most head models assume the skull to be a homogeneous tissue with the same conductivity values in all the directions.
Thus it is important to keep in mind that although the methods to solve the EEG inverse problem are extremely useful, the final solution depends on multiple parameters and the accuracy of choices made.
[1] https://cmontalto.wordpress.com/2013/03/08/what-are-inverse-problems/
[2] Baillet, Sylvain, John C. Mosher, and Richard M. Leahy. “Electromagnetic brain mapping.” IEEE Signal processing magazine 18.6 (2001): 14-30.
[3] Elul, Rafael. “The genesis of the EEG.” International review of neurobiology. Vol. 15. Academic Press, 1972. 227-272.
[4] Lee, Hosuk Sean, et al. “Astrocytes contribute to gamma oscillations and recognition memory.” Proceedings of the National Academy of Sciences 111.32 (2014): E3343-E3352.]