Transfer entropy is a way to estimate interdependencies between two time series that is sensitive to both linear and nonlinear interactions so a useful measure for brain signals. However, it has all the limitations of entropy measures applied to signals like the EEG.
The brain is an interdependent network and assessing interdependency between brain regions is an important aspect of understanding the brain. In my last post I talked about Granger causality which is a linear measure with some limitations when applied to a nonlinear system like the brain. Another way to estimate interdependencies between two time series is within the framework of information theory. Measures based on information theory are sensitive to both linear and nonlinear interactions and thus are more general compared to linear Granger causality. Transfer entropy, proposed by Schrieber and colleagues, aims at quantifying the reduction in uncertainty associated with signal X given signal Y [1]. In fact, it can be shown that transfer entropy is equivalent to Granger causality when applied to a linear system. However, the brain is likely a nonlinear system. Before understanding the concept of transfer entropy, let us review some basic concepts associated with entropy.
The basics of entropy
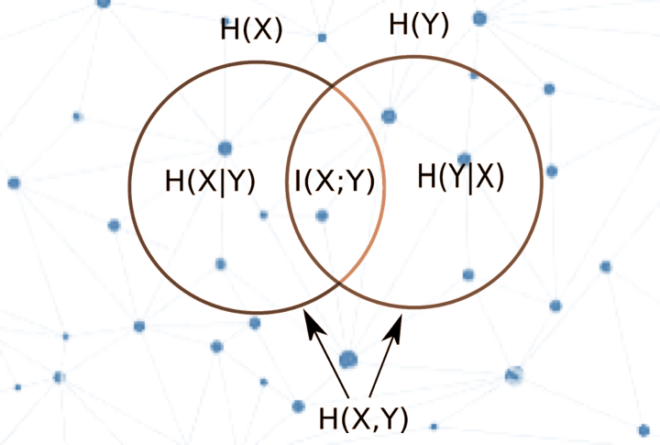
Given a process X, entropy is given as
![]()
Where p(x) is the probability distribution associated with process X. You might think of this as a sum of the probabilities weighted by their log. Since probabilities range from 0 to 1, the log values start at 0 for a probability of 1 and get increasingly negative the smaller the probability. So the more small probability events there are, the bigger the value of H is or higher the entropy, meaning that it is harder it is to predict x and there is therefore more uncertainty.
(See more about entropy here)
Given another process Y, we can analogously define joint entropy as follows:
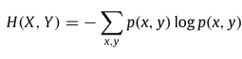
Where p(x,y) is the joint probability = Prob(X=x, Y=y). Joint entropy essentially tells us the uncertainty associated with the joint occurrence of X, Y.
And conditional entropy as:
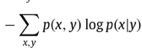
where p(x|y) is the conditional probability or Prob(X=x|Y=y).
Conditional entropy simply tells us how much reduction occurs in the uncertainty associated with X, given the knowledge about Y. If X and Y are independent then, H(X|Y) will be equal to H(X), which is to say that knowing Y does not give us any more information or certainty about what X is at any given time.
Intuitively, we can understand the relation between entropy, joint entropy and conditional entropy with the diagram below, where each circle represents the entropy associated with X, H(X) and entropy associated with Y, H(Y).
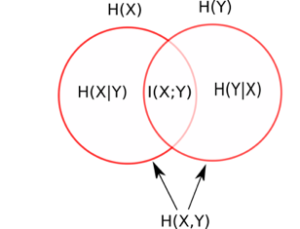
The region where the two circles intersect can be interpreted as mutual information, between X and Y, I(X;Y), which can be understood as the difference between H(X) and H(X|Y) (or equivalently also as H(Y) – H(Y|X) ). Thus I(X;Y) means essentially how much information you can know about X from Y and vice versa.
Now, if X and Y were independent, there would be no overlapping region, and the mutual information would be zero (as H(X|Y) is the same as H(X) since knowing Y tells you nothing about X). In this case the joint entropy H(X,Y) would be equal to H(X) + H(Y). However if there is any overlap or mutual information this can’t be counted twice so the joint etntropy would be H(X) + H(Y)-I(X;Y). Rewritten we get:
I(X;Y) = H(X) + H(Y) – H(X,Y).
At the other extreme, if X and Y are fully dependent (i.e., the two circles fully overlap), then H(X|Y) = 0 (or H(Y|X) = 0), i.e., knowing about Y should theoretically reduce the uncertainty about X to zero (or vice versa). In this situation the mutual information is maximized because knowing X tells you everything about Y and is equal to H(X) (or H(Y)).
Getting to Transfer Entropy
Now that we have some understanding of joint and conditional entropy, let us dive into the concept of transfer entropy. Transfer entropy from Y to X is given as
![]()
Estimating transfer entropy involves computing two conditional entropies, the first one measuring the uncertainty about X at time t+1 given information about X at time t, and the second one measuring uncertainty about X at time t+1 given information about both X and Y at time t. Thus transfer entropy essentially measures the reduction (if any) in the uncertainty associated with X at time t+1 when the information about X is given at time t in addition to that of Y at time t. The transfer entropy from X to Y is defined analogously.
As an illustration of why this can be important in understanding the brain take the following simple example. Imagine that X transmits a signal to Y, and Y in turn processes the signal and feeds it back to X depending on its state at time t . In that case knowing both X and Y together would tell you what you need to know about X at time t, t+1. In other words, if Y has a causal influence on X, then knowing the state of X and Y at time t will minimize the prediction error about the state of X at t+1
It is important to note that transfer entropy is an asymmetric measure, i.e. transfer entropy from Y to X is not equal to transfer entropy from X to Y. Also, transfer entropy is a pairwise measure and in the case of more than two observations, without appropriate conditioning, transfer entropy cannot distinguish direct from indirect causality and in such a case a spurious causality may be inferred.
Pitfalls and limitations when applying it to the EEG
Applying entropy algorithms to a time series like the EEG requires a bit of guesswork into what aspect of the signal may be important and on what time scales, essentially choosing what aspect of your signal constitutes your X. Any measure of transfer entropy is only as good as the assumptions underlying the computation of entropy from the EEG. You can learn more about that in these previous blogposts:
The Impact of Parameter Choice on EEG Entropy Measures
References
[1] Vicente, Raul, et al. “Transfer entropy—a model-free measure of effective connectivity for the neurosciences.” Journal of computational neuroscience 30.1 (2011): 45-67.