Kuinka verrataan ja valitaan paras Bayesin malli EEG-tietojen dynaamisessa kausaalimallinnuksessa tai DCM:ssä?
Kahdessa edellisessä blogissa opimme dynaamisen kausaalimallinnuksen (DCM) peruskomponenteista elektroenkefalografialla (EEG) ja tarkastelimme kahta keskeistä komponenttia – hermomassamalleja ja Bayesin päättelyä melko yksityiskohtaisesti. Tässä kaksiosaisessa blogikirjoituksessa tarkastelemme Bayesin mallivalintaa yksityiskohtaisesti.
Bayes-tekijä
Kuten olemme aiemmin keskustelleet, DCM:ssä on määriteltävä kilpailevia ehdokasmalleja tai hypoteeseja. Siksi tarvitsemme tavan verrata näitä malleja ja valita malli, joka selittää parhaiten tietomme. Yhteenvetona voidaan todeta, että nämä mallit on kuvattu käyttämällä hermomassamalleja, joiden yhteysparametrit ovat tuntemattomia. Bayesin mallin valintaa käytetään DCM:ssä arvioimaan näiden mallien suhteellisia todennäköisyyksiä ottaen huomioon EEG/MEG-tiedot, joiden liitettävyyttä haluamme analysoida, ja mallista saatavilla olevat aiemmat tiedot. Tietylle mallille mi ja MEG/EEG-tiedoille y p(mi|y ) edustaa mallin mi ehdollista todennäköisyyttä datan y perusteella. Jos tällaisia malleja on N, tehtävänä on valita paras malli.

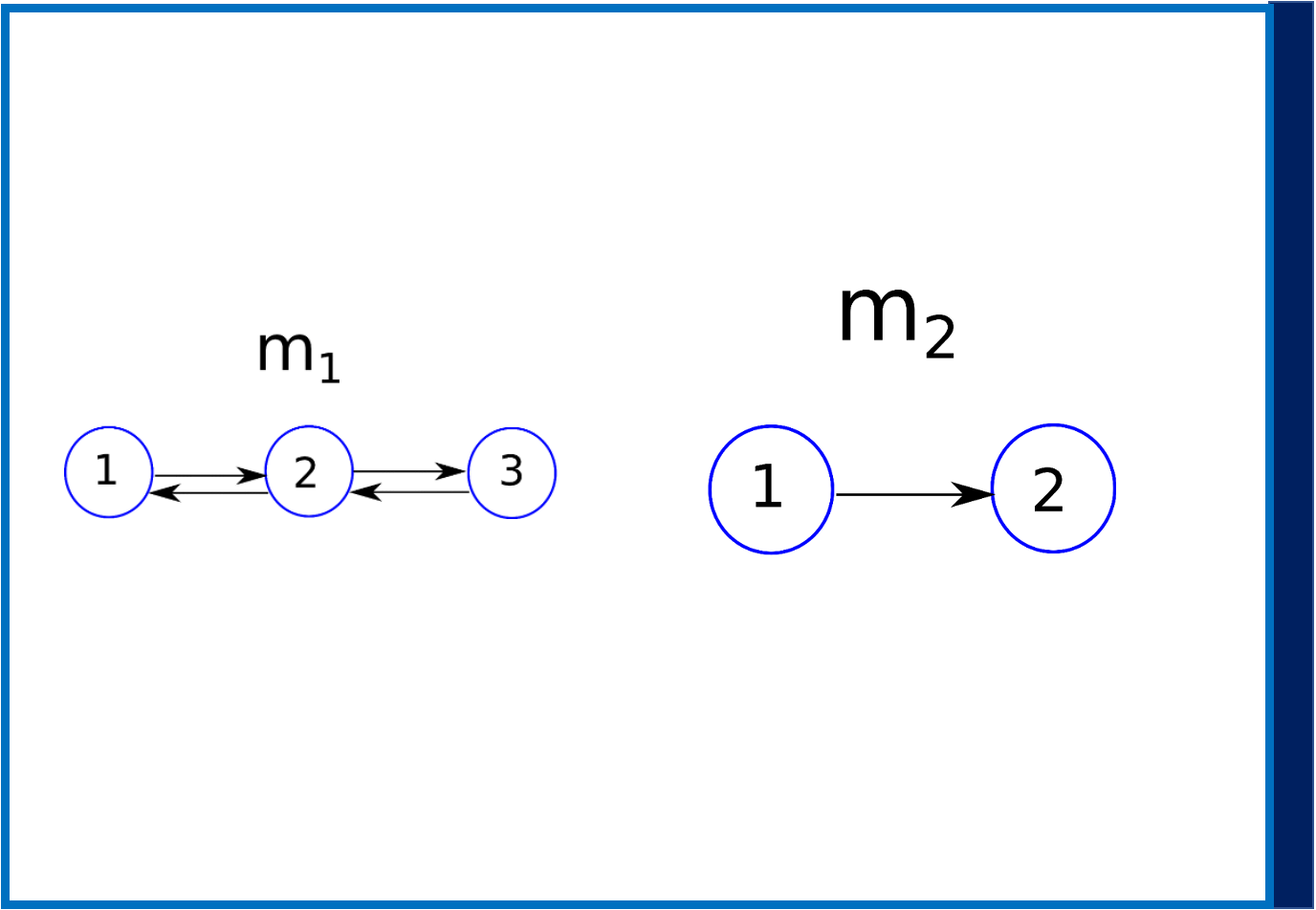
Kuva 1: Kaksi ehdokasmallia m1 , jossa on kolme vuorovaikutteista aivoaluetta, ja m2 , jossa on kaksi vuorovaikutteista aivoaluetta.
Tarkastellaan esimerkkinä, että on olemassa vain yksi malli m1 ja edeltävä p(Θ|m1). Tässä skenaariossa tuntemattomien parametrien posteriorinen jakauma (eli mallin määrittelemä aivoalueiden välinen yhteys) annetaan seuraavasti:
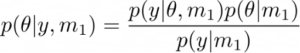
Oletetaan nyt, että yhden mallin sijasta sinulla on kaksi kilpailevaa mallia m1 ja m2 (katso kuva 1). Nyt herää kysymys, mikä on paras malli näistä kahdesta sen jälkeen, kun olemme havainneet tiedot y? Tässä skenaariossa voidaan käyttää Bayesin mallin valintaa. Tämä edellyttää, että laskemme posterioriset todennäköisyydet p(m1|y) ja p(m2|y), mikä yksinkertaisesti osoittaa, että tietojen (ja mahdollisten aiempien) perusteella luotamme enemmän malliin, m1 vai m2? Bayesin lauseesta meillä on,
![]()
Vertaamalla näitä kahta mallia meillä on
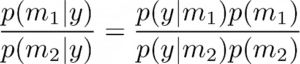
Kahden mallin m1 jam 2 uskottavuutta voidaan siten arvioida käyttämällä rajatodennäköisyyksien p(y|mi) suhdetta, joka tunnetaan myös mallitodisteena ja joka tunnetaan myös nimellä Bayesin tekijä,
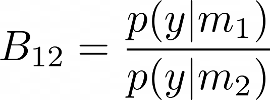
Arvo B12 > 1 voidaan tulkita suosivan mallia 1 mallin 2 kustannuksella, kun otetaan huomioon havaitut tiedot y. Vastaavasti B12 < 1 tarkoittaisi, että haluaisimme suosia mallia 2 mallin 1 sijaan, kun otetaan huomioon tiedot y. Saadaksemme lisää intuitiota tähän, on myös hyödyllistä huomata tässä vaiheessa, että voimme kirjoittaa posterioristen todennäköisyyksien p(m1|y) ja p(m2|y) suhteen seuraavasti:

Yllä olevasta yhtälöstä voimme nähdä, että kahden mallin m1 ja m2 todennäköisyyksien suhde on muuttunut sen jälkeen, kun olemme nähneet tiedot (eli posterioriset todennäköisyydet), annetaan Bayes-tekijänä kerrottuna aiempien mallien todennäköisyyksien suhteena. Näin ollen, riippumatta aiemmista uskomuksistamme näistä kahdesta mallista (saatamme suosia toista mallia toisen kustannuksella ennen kuin näemme tiedot), Bayes-tekijä antaa tekijän, jonka avulla meidän on päivitettävä uskomuksemme kahteen malliin tietojen nähtyä! Toisin sanoen posterioriset kertoimet = Bayes-tekijä X:n aiemmat kertoimet [1]. Bayes-tekijäarvojen tulkinta vertaamalla kahta mallia on esitetty seuraavassa taulukossa [1-2]
| B12 | p(m1|y) | Todisteet m1:n puolesta |
| 1-3 | 0,5-0,75 | Heikko |
| 3-20 | 0,75-0,95 | Positiivinen |
| 20-150 | 0,95-0,99 | Vahva |
| >=150 | >=0.99 | Erittäin vahva |
Näin ollen, kun otetaan huomioon kaksi mallia m1 ja m2, Bayesin kerroin 150 vastaisi 99 %:n uskomusta mallin m1 puolesta, kun taas Bayesin kerroin 3 vastaisi 75 %:n uskomusta.
Seuraavassa blogikirjoituksessa tarkastelemme tulkintaa ja intuition saamista mallitodisteista, joista Bayes-tekijä riippuu. Tarkastelemme myös joitain DCM:n sovelluksia EEG/MEG:ään ja tiettyjä Bayes-kertoimen käyttöön liittyviä ongelmia.
[1] Kass, Robert E. ja Adrian E. Raftery. ”Bayesin tekijät.” American Statistical Associationin lehti 90.430 (1995): 773-795.
[2] https://www.fil.ion.ucl.ac.uk/spm/course/slides14-may/11_DCM_Advanced_1.pdf