¿Cómo se compara y selecciona el mejor modelo bayesiano en Modelado Causal Dinámico o DCM de datos de EEG?
En los dos blogs anteriores aprendimos sobre los componentes básicos del modelado causal dinámico (DCM) con electroencefalografía (EEG) y analizamos dos componentes clave: los modelos de masa neuronal y la inferencia bayesiana con cierto detalle. En esta publicación de blog de dos partes, veremos la selección de modelos bayesianos en detalle.
El factor Bayes
Como hemos discutido antes, en DCM uno tiene que especificar modelos o hipótesis candidatos en competencia. Por lo tanto, necesitamos una forma de comparar eventualmente estos modelos y seleccionar el modelo que mejor explique nuestros datos. Solo para recapitular, estos modelos se describen utilizando una población de modelos de masa neuronal con parámetros de conectividad desconocidos. La selección de modelos bayesianos se utiliza en DCM para evaluar las probabilidades relativas de estos modelos dados los datos de EEG / MEG para los que queremos analizar la conectividad y cualquier información previa disponible en el modelo. Para un modelo dado mi y datos MEG / EEG y, p (mi | y ) representa la probabilidad condicional del modelo mi dados los datos y. Si hay N modelos de este tipo, la tarea es elegir el mejor modelo.

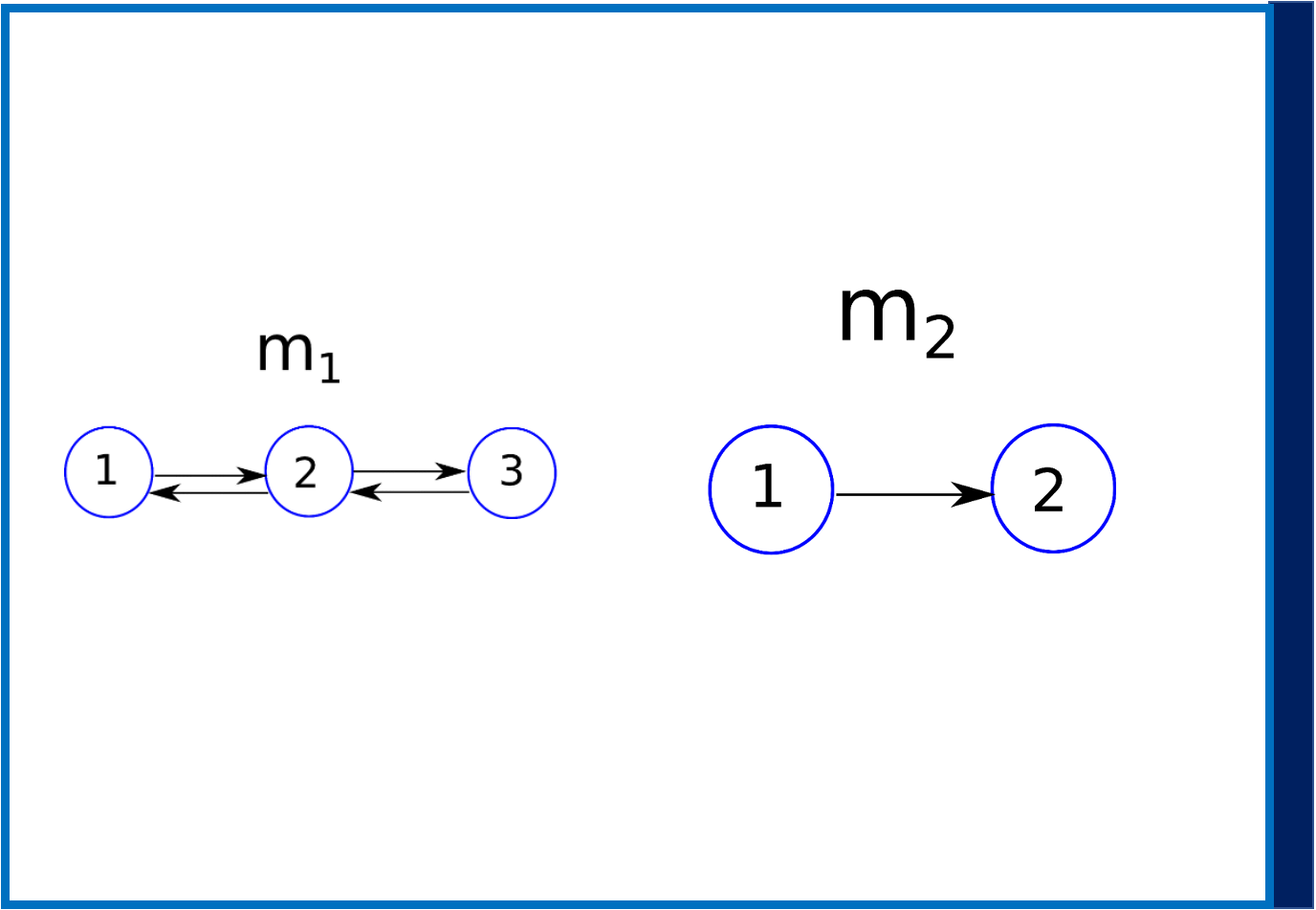
Figura 1: Dos modelos candidatos m1 con tres regiones cerebrales que interactúan y m2 con dos regiones cerebrales que interactúan.
Como ejemplo, consideremos que solo hay un modelo m1 y el anterior p(Θ|m1). En este escenario, la distribución posterior de parámetros desconocidos (es decir, la conectividad entre las regiones del cerebro según lo especificado por el modelo) se da como,
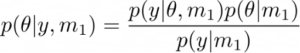
Ahora supongamos que en lugar de un modelo, tiene dos modelos que compiten m1 y m2 (consulte la Figura 1). Ahora surge la pregunta, ¿cuál es el mejor modelo entre estos dos después de haber observado los datos y? La selección de modelos bayesianos se puede utilizar en este escenario. Esto requiere que calculemos las probabilidades posteriores p (m1 | y) y p (m2 | y), lo que simplemente indica que dados los datos (y cualquier anterior), ¿en qué modelo confiamos más, m1 o m2? Del teorema de Bayes tenemos,
![]()
Comparando los dos modelos, tenemos
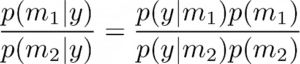
La plausibilidad de los dos modelos m1 y m2 puede evaluarse utilizando la relación de las probabilidades marginales p(y|mi) también conocida como evidencia del modelo, que también se conoce como factor de Bayes,
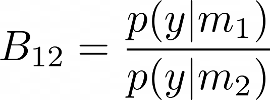
Un valor B12 > 1 puede interpretarse como que favorece al modelo 1 sobre el modelo 2 dados los datos observados y. De manera similar, B12 < 1 significaría que querríamos favorecer el modelo 2 sobre el modelo 1, dados los datos y. Para obtener más intuición sobre esto, también es útil observar en este punto que podemos escribir la razón de las probabilidades posteriores p (m1 | y) y p (m2 | y) como,

A partir de la ecuación anterior, podemos ver que la relación de probabilidades de dos modelos m1 y m2 ha cambiado después de haber visto los datos (es decir, las probabilidades posteriores), se da como el factor de Bayes multiplicado por la relación de las probabilidades de los modelos anteriores. Por lo tanto, independientemente de nuestras creencias previas sobre los dos modelos (podemos favorecer un modelo sobre el otro antes de ver los datos), el factor de Bayes da el factor por el cual tenemos que actualizar nuestras creencias en los dos modelos después de ver los datos. En otras palabras, probabilidades posteriores = factor de Bayes X probabilidades anteriores [1]. La interpretación de los valores del factor de Bayes al comparar dos modelos se da en la siguiente tabla [1-2]
| B12 | p(m1|y) | Evidencia a favor de m1 |
| 1-3 | 0,5-0,75 | Débil |
| 3-20 | 0,75-0,95 | Positivo |
| 20-150 | 0,95-0,99 | Fuerte |
| >=150 | >=0.99 | Muy fuerte |
Así, dados dos modelos m1 y m2, un factor de Bayes de 150 correspondería a una creencia del 99% a favor del modelo m1, mientras que un factor de Bayes de 3 correspondería a una creencia del 75%.
En la próxima publicación de blog, veremos cómo interpretar y obtener algo de intuición sobre la evidencia del modelo, de la que depende el factor Bayes. También veremos algunas aplicaciones de DCM a EEG / MEG y ciertos problemas con el uso del factor de Bayes.
[1] Kass, Robert E. y Adrian E. Raftery. «Factores de Bayes». Revista de la Asociación Americana de Estadística 90.430 (1995): 773-795.
[2] https://www.fil.ion.ucl.ac.uk/spm/course/slides14-may/11_DCM_Advanced_1.pdf