El modelado causal dinámico (DCM) toma un marco bayesiano probabilístico para inferir la conectividad efectiva o causal, esencialmente para modelar cómo un estímulo influiría en la conectividad entre regiones.

En la publicación de blog anterior , analizamos algunos de los aspectos fundamentales del teorema de Bayes. En este blog analizamos una aplicación de un enfoque bayesiano a los datos de EEG / MEG, conocido como modelado causal dinámico (DCM) [1], que se utiliza para inferir una conectividad efectiva. La conectividad efectiva tiene como objetivo estimar la influencia de una región neuronal sobre la otra (es decir, la influencia causal), a diferencia de la conectividad funcional que tiene como objetivo buscar asociaciones estadísticas (o correlaciones) [2].

Comenzando con el problema inverso

DCM se propuso originalmente para el análisis de datos de resonancia magnética funcional, pero en este blog mantendremos el enfoque en los datos de EEG / MEG, ya que los principios subyacentes siguen siendo en gran medida los mismos (excepto por la forma en que se especifican los modelos). La idea principal en el análisis de DCM es sobre la inversión del modelo. Ya estamos familiarizados con el concepto de problemas inversos de EEG, donde el objetivo es estimar la actividad neuronal x, dados los datos de EEG/MEG y. Hemos visto anteriormente que los datos de EEG / MEG se pueden modelar como

Donde L es la matriz de campo principal que captura las suposiciones de cómo las corrientes de los dipolos se transforman en potencial eléctrico registrado en sensores de EEG, x es la actividad neuronal desconocida y n es el ruido de medición. Esto también se conoce como el modelo hacia adelante.

El análisis de DCM arroja este problema en un marco probabilístico, y en lugar de simplemente estimar la actividad neuronal, hace la pregunta: supongamos que el sistema (es decir, el cerebro) está perturbado por un estímulo externo conocido, ¿podemos inferir cómo se ve influenciada la conectividad entre las regiones del cerebro?

Basado en un modelo no lineal de cómo interactúa cada región del cerebro

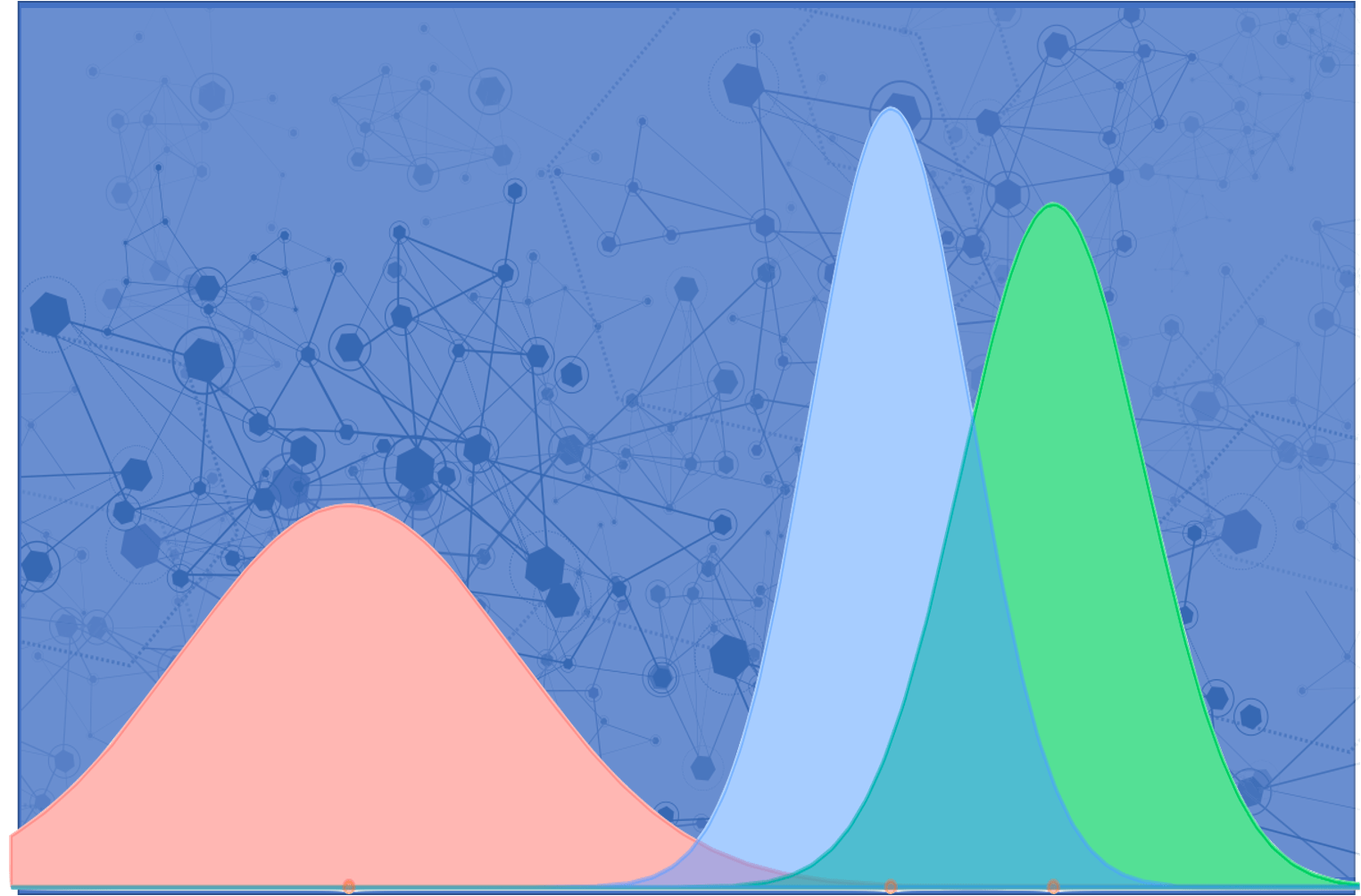
DCM primero asume un modelo de cómo la actividad dentro de cada región del cerebro evoluciona e interactúa entre sí y también explica la presencia de un estímulo. Esto se modela utilizando lo que se conoce como modelos de masa neuronal, que son esencialmente un conjunto de ecuaciones diferenciales no lineales que describen la interacción entre la subpoblación de la región cortical, que puede incluir varias células. Matemáticamente, esto se puede escribir como

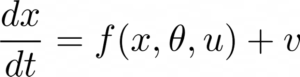
No nos preocupemos por la forma exacta de la función f () (que viene dada por los modelos de masa neuronal), sino que entendamos aquí que DCM asume que los estados neuronales evolucionan en el tiempo de acuerdo con este modelo no lineal, donde u es el estímulo de entrada, Θ son los parámetros del modelo que modelan la conectividad entre las regiones del cerebro (¡y también las conexiones intrínsecas dentro!) y x, los estados neuronales ocultos. Esencialmente, DCM asume un estímulo experimental como una perturbación de la dinámica neuronal y dicho estímulo puede cambiar la conectividad (y la actividad neuronal), lo que se puede inferir utilizando enfoques bayesianos.

Luego, los estados neuronales se propagan a los sensores de EEG, nuevamente de acuerdo con el modelo directo que hemos visto antes.

Un ejemplo de uso de DCM para modelar la negatividad de desajuste

Ahora la tarea en DCM es inferir x y Θ, dado y. Una de las diferencias fundamentales entre DCM y otros enfoques de estimación de conectividad es que, en DCM, debe especificar un conjunto de modelos competitivos (es decir, hipótesis) sobre cómo se generan sus datos. Por ejemplo, considere un ejemplo de experimento de negatividad de desajuste, donde espera ver un pico negativo en el EEG cuando se encuentran sonidos desviados en una corriente de sonidos repetidos y esto ocurre aproximadamente a los 100-200 ms [3]. Otro aspecto de la DCM es que asume que las ubicaciones de las regiones del cerebro se conocen a priori y, en este caso, se cree que están involucradas cinco fuentes sobre las cortezas auditivas primarias izquierda y derecha (A1), la circunvolución temporal superior izquierda y derecha (STG) y la circunvolución frontal inferior derecha (IFG), según la literatura relacionada con la localización de la fuente en la negatividad de desajuste. Lo que se muestra a continuación es un conjunto de tres modelos competidores: modelo F, modelo B y modelo FB. Como puede ver, cada modelo asume que la conectividad debida a un estímulo de entrada que se transmite a través de las cortezas auditivas modula la conectividad entre las regiones del cerebro de una manera diferente. Ahora, ¿en qué modelo confiamos?

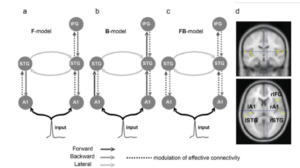
Figura 1: Modelos competitivos para explicar la negatividad de los desajustes [3]

Inferencia bayesiana en juego

Esta es precisamente la pregunta que DCM intenta responder utilizando una combinación de enfoques bayesianos que involucra inferencia bayesiana y selección de modelos. Por lo tanto, dado un modelo m, DCM apunta a la inversión del modelo. En el lenguaje bayesiano, el objetivo es estimar la distribución posterior p(Θ,x|y,u,m), dada la probabilidad (es decir, el modelo directo) p(y|Θ,x,u,m) y alguna distribución de probabilidad previa sobre los parámetros y el estado neuronal, es decir, las creencias de uno sobre este parámetro, antes de que se vean los datos.

Figura 2: Dado un modelo m sobre cómo interactúan tres regiones cerebrales (A, B, C) modeladas utilizando modelos de masa neuronal, donde Θ es la conectividad desconocida entre (o incluso dentro) de las regiones cerebrales y x son los estados neuronales ocultos, DCM tiene como objetivo inferir estas cantidades utilizando el teorema de Bayes, es decir, basado en el modelo de probabilidad y una distribución previa sobre Θ y x.

La siguiente figura resume los principales ingredientes de DCM. En las próximas publicaciones de blog, veremos los modelos de masa neuronal y cómo se realizan realmente la inferencia bayesiana y la selección de modelos dentro de DCM.

Figura 3: Principales pasos involucrados en el análisis de DCM. Figura reinterpretada de diapositivas del curso SPM.

Algunas advertencias

Tenga en cuenta que hay muchas suposiciones en juego en cada paso, desde el comportamiento dipolar de las fuentes hasta el modelo de masa neuronal f () y el conocimiento a priori de las conexiones entre las regiones del cerebro. Además, puede ser difícil especificar modelos competitivos para una gran cantidad de regiones del cerebro. Siempre es bueno examinar las suposiciones y no aceptarlas al pie de la letra.

Referencias

[1] Friston, K. J., Harrison, L. y Penny, W. (2003). Modelado causal dinámico. Neuroimagen, 19(4), 1273-1302.

[2] Friston, K. J. (2011). Conectividad funcional y efectiva: una revisión. Conectividad cerebral, 1(1), 13-36.

[3] Kiebel, S. J., Garrido, M. I., Moran, R. J. y Friston, K. J. (2008). Modelización causal dinámica para EEG y MEG. Neurodinámica cognitiva, 2(2), 121-136.