Un marco bayesiano, que funciona con probabilidades condicionales, tiene numerosas aplicaciones en neuroimagen en general y en EEG específicamente. Pero primero, una introducción al teorema de Bayes y cómo funciona.
El enfoque bayesiano tiene varias aplicaciones en el campo del análisis de datos de EEG. Por ejemplo, varios modelos de interacciones neuronales pueden dar lugar al mismo resultado de EEG. ¿Qué modelo o hipótesis es la más probable? Además, ¿podemos reducir la incertidumbre sobre nuestros modelos integrando el conocimiento del dominio previamente adquirido? Estas cosas (y muchas más) pueden responderse dentro del contexto de un marco bayesiano. Otra aplicación sería formular el problema inverso del EEG de manera probabilística y utilizar el enfoque bayesiano para estimar las distribuciones de las corrientes fuente a partir de los datos del EEG.
Probabilidades frecuentistas versus condicionales
La noción más común de probabilidad con la que estamos familiarizados es que representa la frecuencia de los resultados cuando se realiza un experimento muchas veces. Por ejemplo, si lanzamos una moneda 1000 veces, esperaremos que salga cara unas 500 veces. Esta noción, basada en las frecuencias de eventos a largo plazo, se conoce como la interpretación frecuentista de la probabilidad.
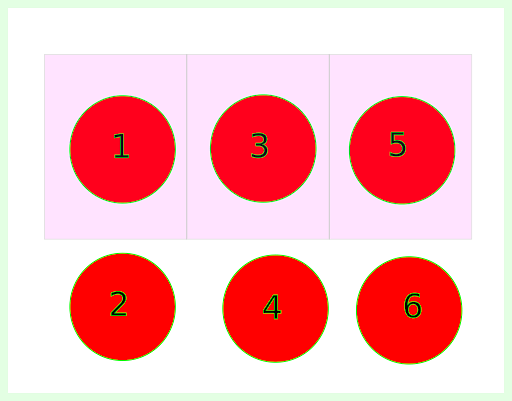
La interpretación bayesiana de la probabilidad se basa en la noción de usar la probabilidad para cuantificar la incertidumbre sobre algo. Antes de comprender lo que significa el teorema de Baye, familiaricémonos rápidamente con las ideas de probabilidades conjuntas, condicionales y marginales. Imagina que hay seis bolas numeradas del 1 al 6. Sea A el evento de recoger la bola número 5 y B el evento de recoger una bola impar (ver Figura 1). 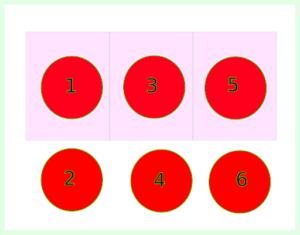
Ahora, si uno puede hacer una pregunta: ¿Cuál es la probabilidad de recoger la bola número 5, dado que ha recogido un número impar? Matemáticamente, lo que pretendemos calcular es P (A | B), es decir, se ha producido la probabilidad de A dado B. Esto parece bastante sencillo de calcular. Dado que sabemos que B ha ocurrido, esto significa que se ha elegido 1, 3 o 5. Ahora la probabilidad de que la bola elegida sea 5 es simplemente 1/3. Esto también se puede dar usando una fórmula,
P(A|B) = P(A,B) / P(B)
Donde P(A,B) es la probabilidad de que tanto A como B hayan ocurrido, que en nuestro caso sería simplemente 1/6 y la probabilidad de que solo haya ocurrido B, es decir, P(B) es 1/2 (porque de seis resultados posibles, solo tres resultados pueden ser un número impar), por lo tanto, P(A|B) = 1/6 / 1/2 = 1/3
El término P(A|B) también se conoce como probabilidad condicional y P(B) se conoce como probabilidad marginal. Una vez puede definir análogamente,
P(B|A) = P(A,B) / P(A)
Teorema de Bayes
Usando las dos ecuaciones anteriores, llegamos al teorema de Baye, que nos dice que
P(B|A) = P(A|B) * P(B) / P(A)
¡De acuerdo! Ahora, ¿qué nos dice esto y cómo es útil? ¿Ahora parece que simplemente estamos multiplicando algunas probabilidades y dividiendo por alguna probabilidad?
Analicemos esta fórmula y lo que puede hacer con un ejemplo concreto. Supongamos que existe una prueba que es capaz de detectar la enfermedad D. Ahora se sabe que la prueba tiene una precisión del 90%. Es decir, 900 de cada 1000 personas que tienen esta enfermedad darán positivo. Además, se sabe que la prueba dará una lectura positiva incluso en ausencia de la enfermedad en el 8% de los casos. También sabemos que es una enfermedad rara y su incidencia en la población es del 1%, es decir, P(D) = 0,01. Por lo tanto, P (D *) = 1-0.01 = 0.99, que denota el porcentaje de la población que no tiene la enfermedad.
Ahora te has hecho la prueba y el resultado ha sido positivo. Es muy probable que creas el resultado. Después de todo, la prueba tiene una precisión del 90%. Sin embargo, ¿es esta una deducción correcta? Bueno, según el teorema de Baye, ¡tienes que refinar un poco tu respuesta!
Visualicemos todo el escenario usando un diagrama. Suponga que tiene la enfermedad y, por lo tanto, pertenece al área roja de la Figura 2. Ahora realiza la prueba y el resultado podría ser +ve o -ve. En este escenario, la probabilidad de que sea positivo es 0,90 ya que la prueba tiene una precisión del 90%, por lo que podemos definir la probabilidad condicional P(+ve|D) = 0,90. En consecuencia, P(-ve|D), es decir, dará negativo dado que tiene la enfermedad tiene que ser 0,10, ya que la probabilidad total debe sumar 1.
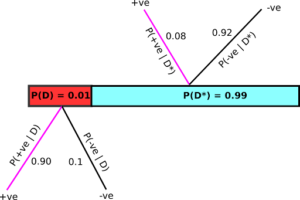
Del mismo modo, si no tiene la enfermedad (y, por lo tanto, pertenece a la sección cian), nuevamente son posibles dos escenarios: dará positivo y la probabilidad de que esto suceda, denotada por P + ve |D*) es 0,08 (ya que sabemos que la prueba da falsos positivos 8 de cada 100 veces). En consecuencia, la probabilidad de que la prueba salga negativa, dado que no tiene la enfermedad, es P (-ve|D*) = 0,92. Ahora que estamos armados con toda esta información y probabilidades, nos interesa saber – ¿Cuál es la probabilidad de que tenga la enfermedad, dado que el cribado i+ve? Es decir, ¿qué es P(D|+ve)? ¡El teorema de Baye al rescate!
Según el teorema de Baye (ver la ecuación anterior)
P(D|+ve) = P(+ve|D) P(D) / P(+ve)
Tenemos acceso a los dos términos en el numerador, es decir, P(+ve|D) = 0,90 y P(D) = 0,01 . ¿Qué pasa con el término P + ve, la probabilidad de detección positiva en general? Podemos calcular esto agregando las ramas de color magenta anteriores, que conducen a la situación de detección positiva sin importar si tiene la enfermedad o no.
Por lo tanto, P + ve) = P + ve |D) P(D) + P(D*)P(+ve|D*) = 0,90*0,01 + 0,99*0,08 = 0,0882. Conectando estos valores a la ecuación anterior, llegamos a P(D|+ve) ≈ 0.10 . En otras palabras, si da positivo, solo tiene alrededor de un 10% de posibilidades de tener la enfermedad, ¡a pesar de que la precisión de la prueba es del 90%!
En terminología bayesiana, P(D|+ve) se conoce como probabilidad posterior y P(D) se conoce como creencia previa. Ahora puede reducir enormemente su incertidumbre, haciéndose la prueba nuevamente, ya que su probabilidad previa de tener una enfermedad, P (D), ahora es del 10 por ciento en lugar del 1 por ciento. Si su segunda evaluación también resulta positiva, la aplicación del teorema de Bayes ahora producirá P (D | + ve) = 0.53, es decir, ¡53%! Por lo tanto, iterar el teorema de Bayes utilizando creencias previas actualizadas puede proporcionar información extremadamente precisa. Por el contrario, la interpretación frecuentista no intenta calcular cantidades como P(enfermedad|+ve).
En las próximas publicaciones de blog, veremos algunas de las aplicaciones del teorema de Baye en el análisis de datos de neuroimagen.