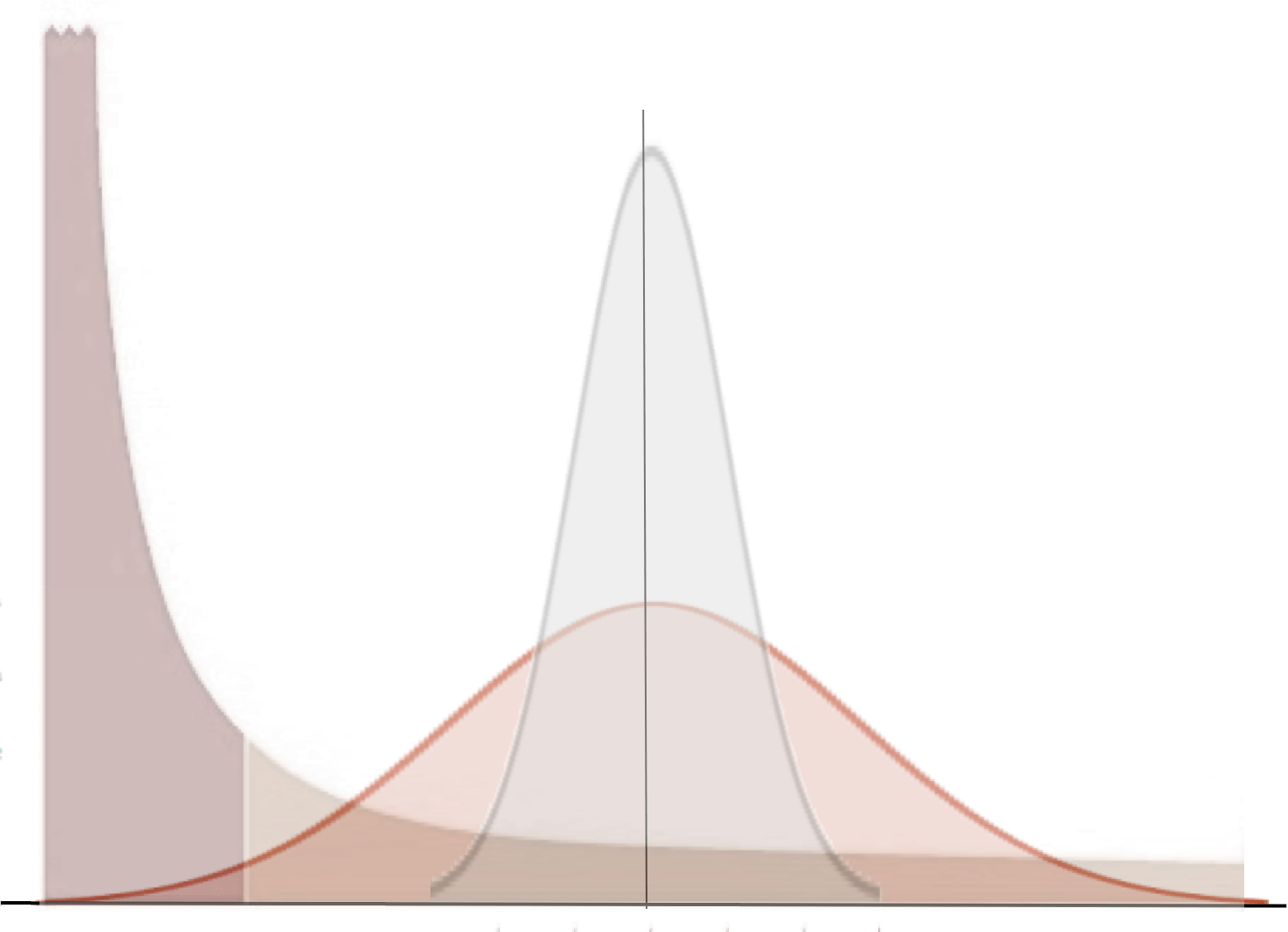
La variabilidad inter e intra persona en las métricas cerebrales en toda la población puede resultar en una interpretación engañosa de los resultados. Es importante comprender las distribuciones de estas métricas en la población.

En toda la literatura científica, la forma más común de representar datos es comparar una métrica particular en dos muestras como un gráfico de barras que muestra las medias de cada grupo con una barra de error que es la desviación estándar o el error estándar de la media y calcular un valor p utilizando una prueba t de estudiantes estándar. Es probable que el artículo tenga un texto que indique que «Hubo una [MÉTRICA DE INTERÉS] significativamente mayor en las personas del [GRUPO1] en relación con el [GRUPO2] (p<0,05)’.

Con el propósito de ilustrar, usemos un ejemplo más concreto de la siguiente manera (con la advertencia de que esto no pretende describir un resultado real, sino simplemente ponerlo en palabras más específicas para que sea más fácil de leer):

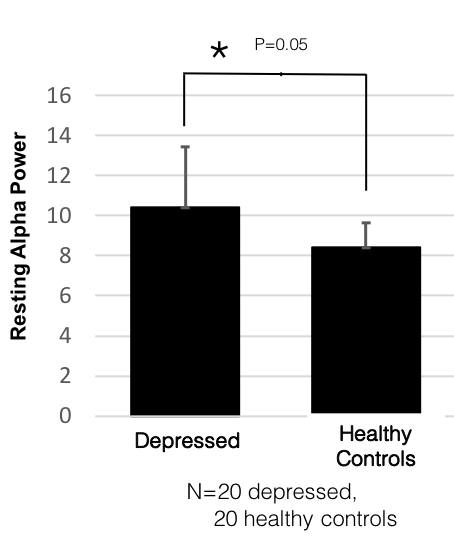
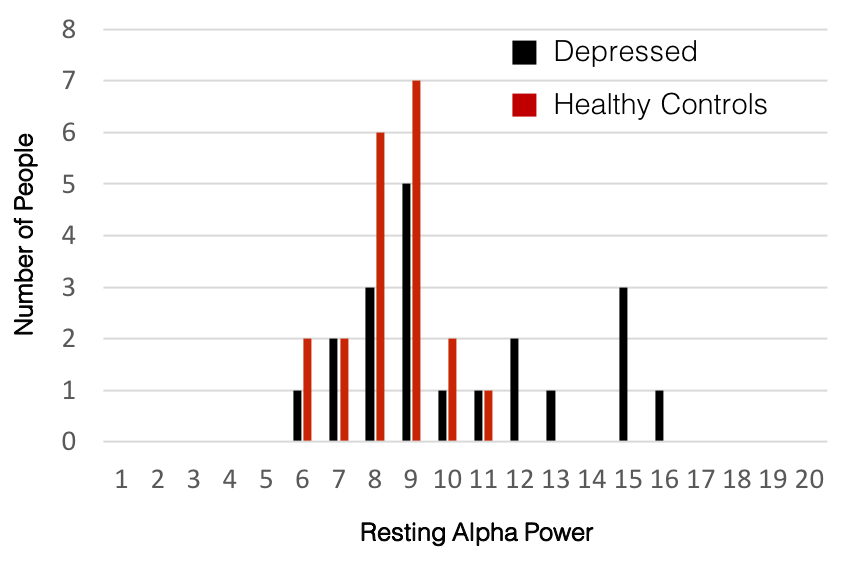
Hubo un poder de banda alfa en reposo significativamente mayor en personas con depresión en relación con los controles sanos (p<0,05).

Retomando esto, los medios podrían tener un titular:

Los investigadores encuentran una diferencia clave entre los cerebros deprimidos y los normales!!!!

Un estudio mostró que las personas con depresión tienen un mayor poder de banda alfa en relación con los controles sanos…

¿Cuál es el problema con esto?

Hay múltiples problemas con esta interpretación. Primero, las distribuciones de ambos grupos probablemente se superponen mucho, por lo que muchas personas en el grupo de control pueden tener valores más altos de la métrica en relación con muchos en el grupo deprimido. Los pequeños cambios de población no pueden interpretarse a nivel individual, este es un problema importante en sí mismo. Sin embargo, aquí discutiremos un tema diferente, que es que, dependiendo de la variabilidad de la métrica particular en la población, el resultado y su interpretación pueden ser completamente erróneos, incluso a nivel de población.

La razón principal es que esta interpretación asume que la métrica de interés se distribuye normalmente en la población. Esta es una suposición peligrosa. Ningún estudio proporciona aún una visión suficiente de la distribución global de varias métricas cerebrales. Con una población adulta de unos 5 mil millones de personas y un tamaño promedio de la muestra de estudio de 40 sujetos que generalmente no son representativos de la demografía global, esto representa una muestra de solo ~ 0.0000008% o menos de 1 de cada 10 millones de personas. Además, normalmente estas muestras están sesgadas geográfica y demográficamente.

Aquí hay algunos ejemplos que ilustran cómo las diferentes distribuciones subyacentes pueden invalidar las conclusiones a nivel de población a las que se llegó como se indicó anteriormente.

Una distribución sesgada

Imagina una situación en la que estás comparando dos grupos. Si la métrica de interés varía entre individuos de acuerdo con la misma distribución de cola larga para ambos grupos, como cualquiera de las distribuciones en el siguiente ejemplo, es fácil encontrar significado donde no lo hay.

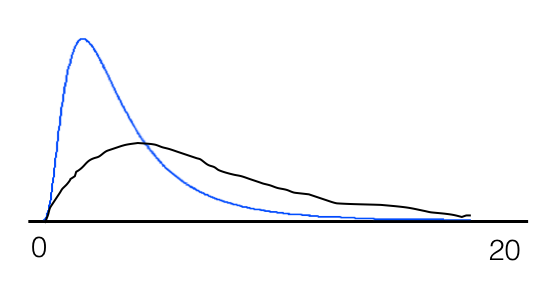La comparación de dos conjuntos de 20 muestras de dicha distribución le dará una prueba t de <0.05 una fracción del tiempo, como en este ejemplo a continuación, aunque la distribución subyacente sea común.

Si sigues repitiendo este experimento, dibujando 20 personas diferentes cada vez, mientras que la mayoría de las veces dibujarás desde la izquierda de la distribución dándote la impresión de que tienes una distribución más o menos normal, elegirás una variedad variable de personas en puntos posteriores de la cola con probabilidad decreciente. A veces tendrás a alguien en el otro extremo de la cola que cambiará sustancialmente la media y la desviación estándar. Este no es un «valor atípico» inexplicable que deba descartarse, sino más bien un indicio de un gran error de muestreo. De hecho, dependiendo de la longitud de la cola, si se repite el muestreo cientos de veces y se comparan las muestras mediante la prueba t, se puede acabar con un resultado significativo (en cualquier dirección) incluso más del 20% de las veces si se tienen ciertos tipos de sesgos de muestreo en el diseño (por ejemplo, para la distribución de la población refleja algunos criterios demográficos subyacentes que se pasaron por alto y se extrajeron sistemáticamente controles de un grupo como estudiantes universitarios, sino el otro grupo del hospital al otro lado de la ciudad). Esto podría explicar fácilmente parte de la variabilidad y la falta de reproducibilidad en los resultados que afecta al campo.

Cambiar distribuciones con la misma media

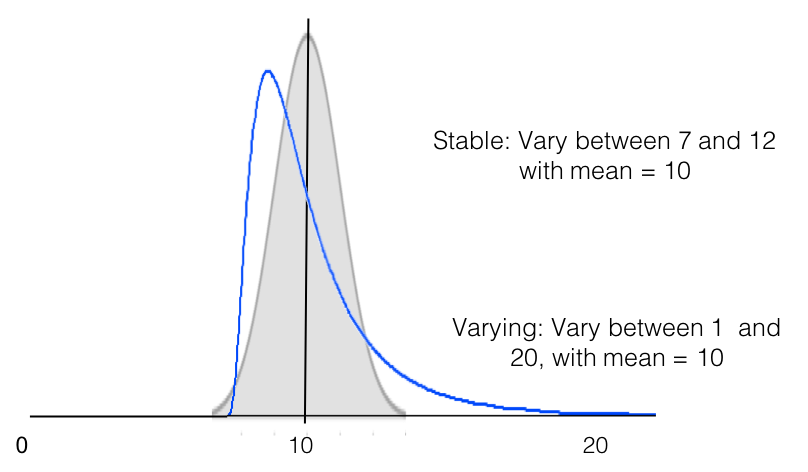
Otra situación que puede surgir es que la distribución cambie mientras que la media permanece igual. En este caso, no encontrará ninguna diferencia significativa a pesar de que hay un cambio sustancial y significativo. Imagina una situación en la que estás comparando dos grupos de la población. Ambos tienen distribuciones normales, pero en un grupo la métrica es más estable, mientras que en el otro varía más, como en el siguiente ejemplo.

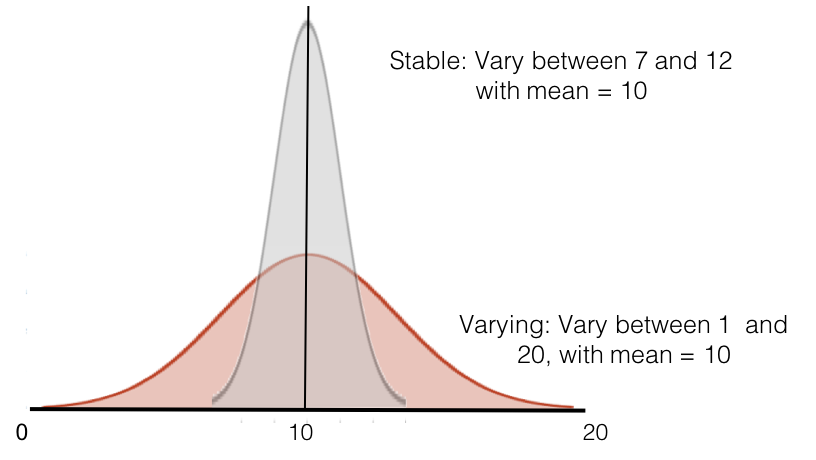Por ejemplo, tal vez el grupo 1 son controles normales, mientras que el grupo 2 es bipolar, donde la métrica fluctúa dentro de los individuos con más frecuencia. En este caso, es probable que muestree a diferentes personas en diferentes puntos de su trayectoria para el trastorno bipolar, lo que resultará en una distribución más amplia de la misma métrica. En este caso, concluirá que no hay diferencia entre los dos grupos.

Sin embargo, puede ver aquí que hay una gran diferencia entre los dos grupos en términos de variabilidad, pero una prueba t entre grupos para 20 muestras aleatorias de cada grupo nunca será significativa ya que la prueba t prueba una diferencia en las medias.

Otra situación que podría surgir es que la distribución en sí cambie o sea diferente entre los dos grupos, mientras que las medias siguen siendo las mismas, como se muestra a continuación. Esto sugiere que, si bien los dos grupos tienen la misma media y aparecerán como «no significativamente diferentes» en una prueba t, algo es bastante diferente entre ellos.

¡Traza la distribución!

Estos son solo un par de ejemplos simples, pero el punto principal es que necesitamos una escala más grande y un mejor muestreo y es imperativo que comprendamos las distribuciones subyacentes a la variabilidad interindividual e intraindividual en las poblaciones. Sin embargo, en la práctica, si bien podemos aumentar nuestros N, las muestras mucho más grandes son costosas y difíciles de recolectar en el contexto de un doctorado o postdoctorado. Aún así, las muestras pequeñas pueden insinuar varias distribuciones. En nuestras propias muestras de datos de EEG de unos pocos miles de personas, por ejemplo, hemos encontrado que diferentes métricas pueden tener distribuciones muy diferentes. Algunos son normales. Muchos están sesgados o tienen cola larga. Otros son de naturaleza bimodal. Por lo tanto, si bien los tamaños de muestra más grandes de 100 a 1000 a millones con un muestreo más amplio de la población a través de varios criterios demográficos son probablemente esenciales para obtener conclusiones confiables, trazar la distribución de su conjunto de muestras en lugar de solo medios, al menos puede indicarle la dirección correcta. La elección de una prueba estadística adecuada y la extracción de conclusiones de ella dependen fundamentalmente de la forma de la distribución de la variabilidad.

Entonces, en pocas palabras, como mínimo, es importante que abandonemos el gráfico de barras y grafiquemos las distribuciones, teniendo en cuenta sus implicaciones.